There’s nothing I hated at high school more than Maths.
Not only were my teachers like something straight out of ‘Summer Heights High’, but the content itself was hard. Really hard.

Even when I deluded myself into believing that I understood a concept, I was hit by a right hook of reality when I got to the exam and couldn’t solve one equation.
Like the time I only just passed a graphs assessment because I drew my parabola like this:
But the story doesn’t end here.
Just when I thought I had escaped Maths when I finished high school, I had to relive the torture at tertiary level.
However, fortunately for me, I had an epiphany.
Somehow, in the midst of re-learning Maths, I actually started learning Maths. In fact, I got a top mark in the course.
How?
I studied Educational Psychology at Uni. It wasn’t until I looked at the latest neuroscience around learning that I was able to overcome my Math-phobia, and actually began, well… enjoying it.
And in the spirit of your classic “I-AM-living-proof” inspiration cliche – if I can do it, you can too.

Here are four, research-backed strategies about how you can get over your aversion to Maths, once and for all.
Focus on concepts over steps
Often when we study Maths, we focus on the steps, instead of the formula or principle.
For example, the standard method for my own Maths learning usually went like this:
- Look at question.
- Look at example steps in the book.
- Write (copy) out the step, subbing in the numbers from the example with the numbers from the question.
- Then rinse and repeat.
Sound familiar? Basically, I was just trying to Maths by learning the steps on how to solve a problem. This resulted in me getting a Fat Not Achieved in my Level 2 Calculus exam.
Why? When I opened my exam to find questions that were worded differently from the ones I had memorised, I was stumped.

Psychology explains this issue pretty well. In our brains, we have two types of knowledge – factual/conceptual knowledge (concepts), and procedural knowledge (the steps).
Learning steps on how to do something by itself – without conceptual knowledge – means that your brain can’t process the information in the optimal way. Why? Because you have no context.
You brain is organised like a filing system. Understanding concepts allows your brain to organise the steps in most efficient way possible, and that way you can more easily access the information, and apply it to new contexts.
It’s like learning a language. Imagine if you had to learn French by memorising whole sentences, rather than learning what the words meant, the grammar rules, the word structures and other important language concepts.
Your chances of French fluency would be gone faster than you could say j’en ai plein le cul.
So, how do we make sure we’re learning concepts properly?
The “Textbook Method”.
This method involves pretending you are writing a textbook/study guide to teach another student.
Instead of just mindlessly copying down the steps as you’re solving an equation, add a column to the right that explains – in simple terms – exactly why you are doing each step.
For example, instead of:
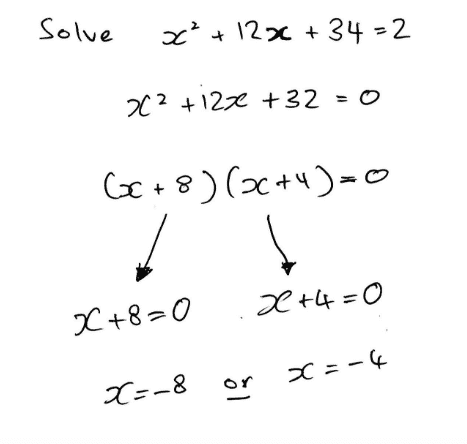
Do this:
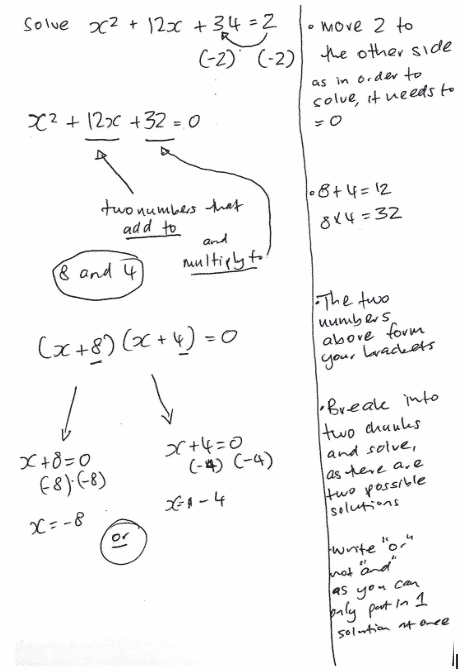
By doing this, you are forced to think about the concepts underneath the steps.
Not only that, but when you go back to your notes in 3 months and can’t remember anything, you’ll have written your notes in a way that you’ll be able to reteach yourself based on the notes. Too easy.
Break down big skills and concepts into small ones, and practice them HARD
Our mind can only juggle so many different thoughts/short-term information at once.
Our long-term memory can store an almost unlimited amount of information, but the issue is that we can’t think about too many things at once. We have to space ‘em out.
Think of studying like RAM on a computer – if you have too many apps or tabs open at once, your computer overloads and freezes.
This is the same with your brain, and is called cognitive overload.

When we try to practice a new skill in Maths, we often experience cognitive overload. Sometimes we don’t realise this until we get into an exam without our notes around, or we get a question that has a twist in it.
When we get a question with a twist in or in an unknown context, our brain is already experiencing a really high level of cognitive load due to having to juggle all dat Maths knowledge in our head.

When we experience a twist, our brain runs out of cognitive processing space and we experience cognitive overload, which prevents us from being able to successfully solve it.
The best way of solving this issue is by breaking down a big skill and concept into micro-skills or micro-steps and over-learning them.
When you’ve properly learned a concept, you’ll know, because it will feel almost automatic.
At this point, that skill does not take up much cognitive load in your brain, and so frees up cognitive processing that you can instead use to put the steps together in your head, or to interpret questions with a twist or in an unknown context, which is often the Merit and Excellence level stuff.
Think of it like boxing. You don’t learn combos on day one; instead, you learn each type of punch until you get the technique right and it’s automatic, and then put it together into a combo.
Here’s how to do this in practice.
When learning how to solve a quadratic equation – instead of tackling it as one skill – break it up into micro-skills and over-learn each one:
- Knowing what a quadratic equation looks like.
- Knowing that a quadratic equation has to equal 0 to solve it, and why.
- Rearranging a quadratic equation to equal 0 when it doesn’t.
- Factorising quadratics [this could even be broken down into further micro-skills].
- Finding the two values of x.
- Explaining why there are two values of x.
- Being able to show the solutions as a parabola.
By doing this, you free up that cognitive processing space in your brain, making it more likely you’ll be able to solve that tricky merit or excellence problem.
Use your notes in small doses
When we can’t remember something, often it’s not an issue of not having the information in our brain, it’s because we’re not able to access it.

For example, you might forget that time you tried to ask out that cute girl in the middle of The Courtyard at Readings Cinema, and got publicly denied – until you hear “Shape of You” by Ed Sheeran and it all comes flooding back. Ed Sheeran’s smooth, sultry tones acted as cue for accessing that memory, no matter how much you wanted to forget it.
How does this relate to learning Maths?
When I first tried studying Maths, I would always have my notes open when practicing. As I mentioned earlier, the teacher would write down something on the whiteboard, I’d read the steps, I’d open up my trauma-inducing Gamma Maths Textbook and do the first question.
I’d use the notes on the board to basically do the same thing but with different numbers, tricking myself into thinking that I was actually understanding it.
Then I’d get to the exam and completely forget everything. Why? Because I didn’t give my brain practice at accessing the knowledge, without seeing it directly in front of me.
When we practice without our notes, there’s a 99% chance we’re going to feel incredibly dumb when we realise we only remembered 20% of what we just learned literally 25 minutes ago.
However, an amazing thing happens when you learn with no book first. We actually start learning.
It goes a little like this:
Brain: attempts to solve problem
Brain: cannot solve problem, because lack of notes
Eyes and brain: reviews notes of concept, and corrects where we went wrong
Brain filing manager: reorganises this knowledge in optimal format in brain
Brain, attempting same problem next time: “I’m so glad I know exactly where to go to access this information, instead of relying on a false sense of knowledge provided by my subject notes!”
By testing our knowledge, failing, then correcting what we did wrong with our notes, we help our brain to build the right mental structures for quick access, which means that we’ll be able to retrieve the information faster and easier next time.
So, use your notes in small doses. It’ll feel hard and awkward at first, and then over time, you’ll actually learn to remember and do the skill or question under pressure.
Practice, but mix it up
In 2013, a bunch of psychologists got together and did a grand study of thousands of studies around learning strategies to find the best ones.
What was one of the top strategies?
Practice. Practice (without your notes, see above) is basically the best thing you can do to learn Maths. However, in order for your practice to work, it needs to be mixed.

What do we mean by mixed? If we just practice the same type of question again and again, it’s less effective than if we try to practice a 3-4 different types of questions at once.
Often, when we learn Maths, we just practice 1-2 types of questions at once, meaning that we don’t get the most benefit out of our practice. Textbooks lay out questions by giving you 20 of one type, then 10 of another type, then 10 of another – and so on.
But by the time we’ve exhausted ourselves studying, we’ve only practiced 15 of one type of question.
If there were four types of questions, your textbook lays it out like this:
AAAAAAAAAAAABBBBBBBBBBBBBCCCCCCCCCCCDDDDDDDDDDD
Instead, it’s much better if you do a couple of one type, then move onto a couple of another type, and then come back to a couple of the first type, like so:
AABBCCAABBCCBBCCDDBBCCDDCCBBDD
By mixing up your practice like this, you get better at applying the same skill or concept across many types of questions, and so you’re more likely to understand the concept and apply it to an unknown style of question in your exam.
The bottom line
Maths is a skill, and like any skill, it’s all about the way you learn it.
Did you learn how to play an instrument by copying out notes on the steps to play guitar?
No, you tried to understand guitar and musical concepts, you practiced the micro-skills until you could do them without thinking, you practiced without your notes/music book open, and you mixed up the type of practice you did.
Sound familiar? These are the four strategies we covered in this post.
For some reason we seem to approach Maths differently, and wonder why we find it hard to learn and understand it.
Give these four strategies a crack when learning Maths, and after a bit of practice – you’ll never look back.

0 Comments